The LibreTexts libraries are Powered by MindTouch ® and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot We also acknowledge previous National Science Foundation support under grant numbersTan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx math Prove that the equation Is an identity Sec^4x Tan^4x = Sec^2x Tan^2xEstablish the identity sin 0( tan 0 cot 0)= sec 0 Write the left side in terms of sine and cosine sin e Simplify the expression inside the parentheses from the previous step and write the result in terms of sine and cosine sin e Simplify the expression from the previous step and write the result in terms of cos 0
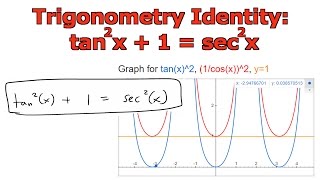
Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube
Tan^2x-sec^2x in terms of sine and cosine
Tan^2x-sec^2x in terms of sine and cosine-I am trying to express this problem in terms of sin/cos and simplify I couldn't figure out where to go, I tried as best I could I know the answer is 1 but I am more interested to know how to do this problem $$ \tan^2x \sec^2x $$ $$ (\sin x / \cos x)^2 (x / \cos x)^2 $$In this video, I show how with a right angled triangle with hypotenuse 1, sides (a) and (b), and using Pythagoras' Theorem, thatcos(x) = 1 / sqrt( 1 tan^2
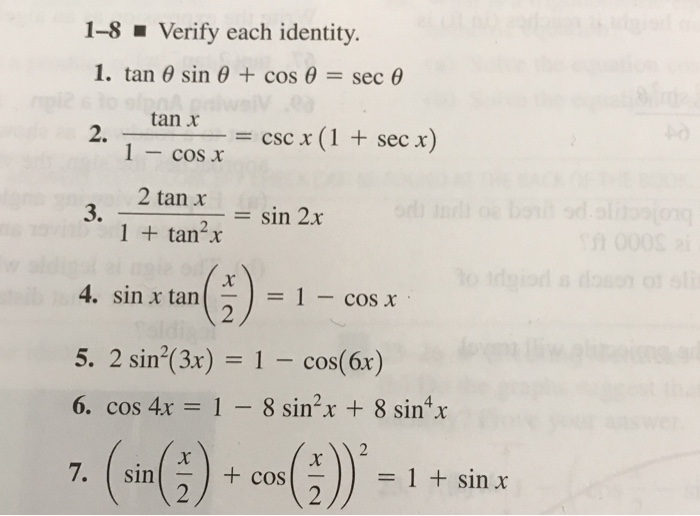



1 8 Verify Each Identity Sec 8 1 Tan 8 Sin 8 Chegg Com
Trigonometric Simplification Calculator \square!Sin(2A) = sin(A)cos(A) cos(A)sin(A) = 2sin(A)cos(A) It is common to see two other forms expressing cos(2A) in terms of the sine and cosine of the single angle A Recall the square identity sin 2 (x) cos 2 (x) = 1 from Sections 14 and 23 This identity can be rewritten asSimplify sin(2x)tan(x)cos(2x) Simplify terms Tap for more steps Simplify each term Tap for more steps Rewrite in terms of sines and cosines Combine and Simplify the numerator Tap for more steps Apply the sine doubleangle identity Combine exponents Tap for more steps Raise to the power of
To rewrite the sine function in terms of tangent, follow these steps Start with the ratio identity involving sine, cosine, and tangent, and multiply each side by cosine to get the sine alone on the left Replace cosine with its reciprocal function Solve the Pythagorean identity tan 2 θ 1 = secGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! sec^2 x tan^2 x = 1 Note that sin^2 x cos^2 x = 1 Hence cos^2 x = 1 sin^2 x and we find sec^2 x tan^2 x = 1/cos^2 x sin^2 x/cos^2 x color(white)(sec^2 x tan^2 x) = (1 sin^2 x)/cos^2 x color(white)(sec^2 x tan^2 x) = cos^2 x/cos^2 x color(white)(sec^2 x tan^2 x) = 1
Start studying Trig equations Learn vocabulary, terms, and more with flashcards, games, and other study tools cos^2xsin^2x (sin) cos2x= 12sin^2x (cos) cos^2x= 2cos^2x1 Sets with similar terms Verklienwoorde 40 terms harvettk22 IBD aminosalicylate derivates 10 terms hiraskhan Sin, Cos, Tan Equations 12 terms michellebarthStart studying Pythargorean Identities Learn vocabulary, terms, and more with flashcards, games, and other study tools4 Chapter 10 Techniques of Integration EXAMPLE 1012 Evaluate Z sin6 xdx Use sin2 x = (1 − cos(2x))/2 to rewrite the function Z sin6 xdx = Z (sin2 x)3 dx = Z (1− cos2x)3 8 dx = 1 8 Z 1−3cos2x3cos2 2x− cos3 2xdx Now we have four integrals to evaluate Z 1dx = x and Z




Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic
Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be usedQuestion Write the trigonometric expression in terms of sine and cosine, and then simplify tan2 x − sec2 x In this section we are going to look at quite a few integrals involving trig functions and some of the techniques we can use to help us evaluate them Let's start off with an integral that we should already be able to do ∫cosxsin5xdx = ∫u5du using the substitution u = sinx
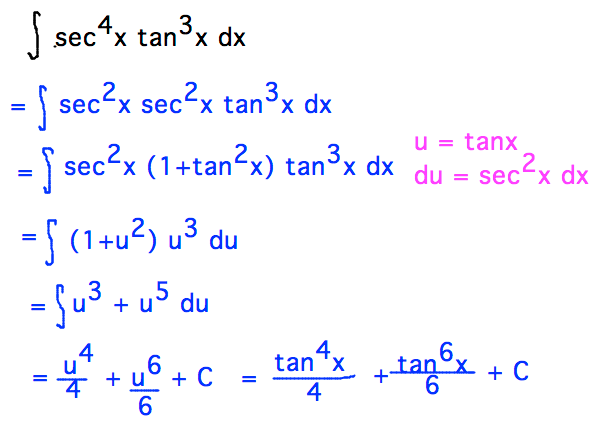



Geneseo Math 222 01 Trigonometric Integration




Trigonometric Integrals
So far in this course, the only trigonometric functions which we have studied are sine and cosine Today we discuss the four other trigonometric functions tangent, cotangent, secant, and cosecant Each of these functions are derived in some way from sine and cosine The tangent of x is defined to be its sine divided by its cosine tanx = sinx cosxSolve for x sin(2x)=tan(x) Rewrite in terms of sines and cosines Rewrite the equation as Solve for Rewrite in terms of sines and cosines Multiply the numerator by the reciprocal of the denominator Multiply and The cosine function is positive in the first and fourth quadrants Tan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx PreCalc 1) Use an Addition or Subtraction Formula to write the expression as a trigonometric function of one number cos 12° cos 18° − sin 12° sin




Directions Simplify The Given Trigonometric Expr Gauthmath




Copyright C Cengage Learning All Rights Reserved 7 Techniques Of Integration Ppt Download
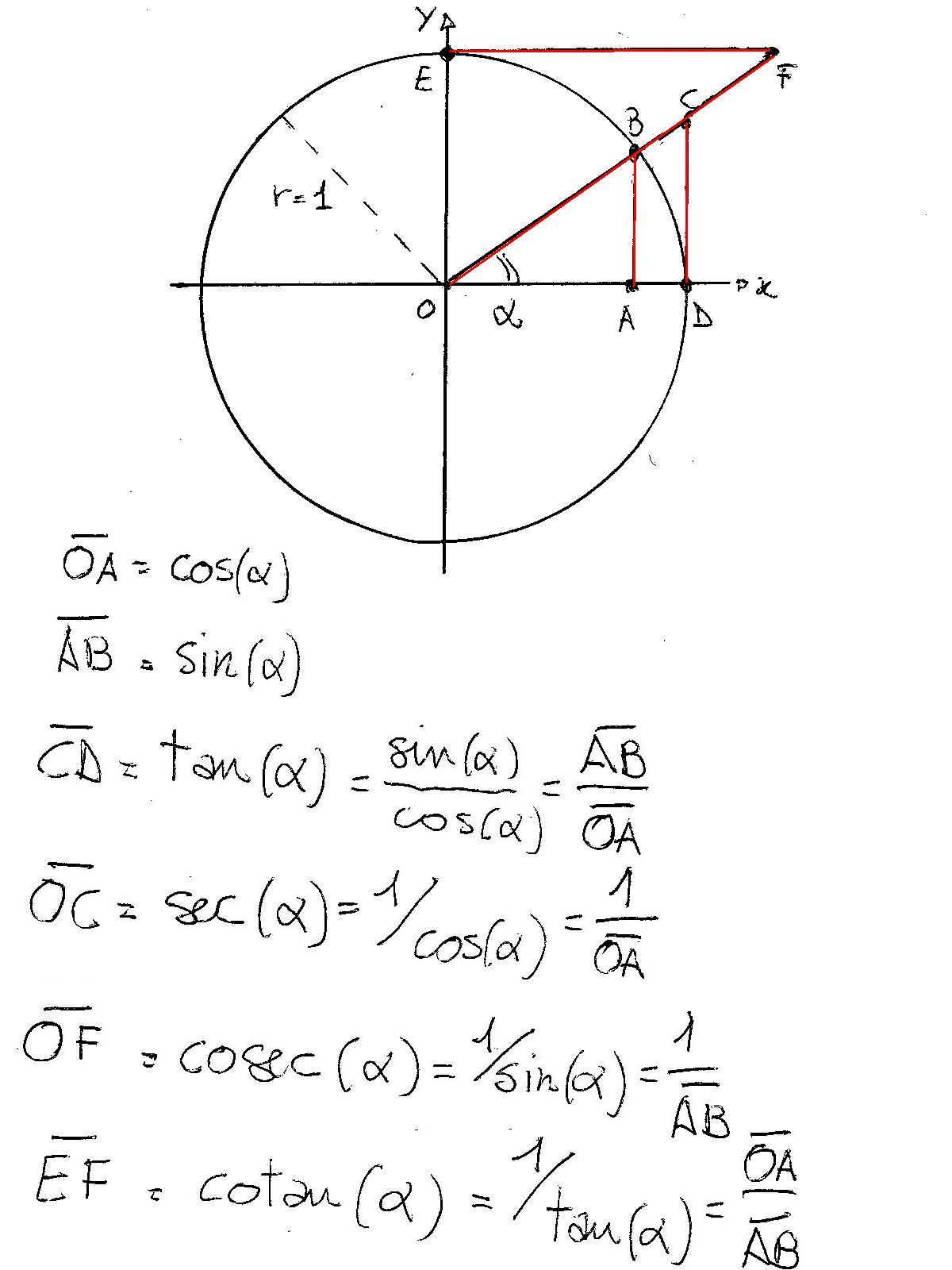
Cos θ as `"adj"/"hyp"`, and tan θ as `"opp"/"adj"`, but we are using the specific x, y and rvalues defined by the point (x, y) that the terminal side passes throughCos hypotenuse q= hypotenuse sec adjacent q= opposite tan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any angle sin 1 y q==y 1 csc y q= cos 1 x q==x 1 sec x q= tan y x q= cot x y q= Facts and Properties Domain The domain is all the values of q that can be plugged into the function sinq, q can be any Write the trigonometric expression in terms of sine and cosine, and then simplify tan2 x − sec2 x;



Basic Trigonometric Functions Trigonometry Socratic



Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Analytic Math2412 Double Angle Power Reducing Half Angle Identities Pdf
cos(ax)cos(bx) = 1 2cos((a − b)x) 1 2cos((a b)x) These formulas may be derived from the sumofangle formulas for sine and cosine Example 726 Evaluating ∫ sin(ax)cos(bx)dx Evaluate ∫sin(5x)cos(3x)dx Solution Apply the identity sin(5x)cos(3x) = 1 2sin(2x) 1 2sin(8x)Solution Using identities \({\sin ^2}x = {\large\frac{{1 – \cos 2x}}{2}\normalsize}\) and \({\cos ^2}x = {\large\frac{{1 \cos 2x}}{2}\normalsize},\) we can writeTrigonometric Identities Solver \square!
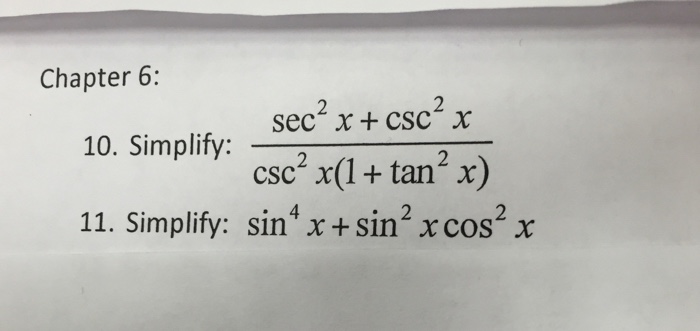



10 Simplify Sec 2x Csc 2x Csc 2x 1 Tan 2x 11 Chegg Com




Sec2x In Terms Of Tanx Trig Identity Youtube
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! Using the double angle identity cos 2 x = 1 − 2 sin 2 x \cos 2 x = 12\sin^2 x cos 2 x = 1 {\sec x \tan x \csc^2 x} The solutions to this equation of motion can be found in terms of functions called elliptic integrals, which are difficult to work with by hand However, employing the smallangle approximation,Sec 2 t = 1 tan 2 t Identities expressing trig functions in terms of their supplements sin( – t) = sin t cos( – t) = –cos t tan( – t) = tan t Difference formulas for sine and cosine sin (s – t) = sin s cos t – cos s sin t cos (s – t) = cos s cos t sin s sin t Sum, difference, and double angle formulas for tangent



Integrate Sec 2x Method 2




Write The Expression In Terms Of Sine And Cosine And Chegg Com
Definitions Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse The six trigonometric functions are defined for every real number, except, for some of themSin(x)= 1 csc(x) cos(x)= 1 sec(x) tan(x)= 1 cot(x) Warning The reciprocal of sin(x) is csc(x), not sec(x) Note We typically treat "0" and "undefined" as reciprocals when we are dealing with basic trigonometric functions Your algebra teacher will not want to hear this, though! For an angle in standard position, we define the trigonometric ratios in terms of x, y and r `sin theta =y/r` `cos theta =x/r` `tan theta =y/x` Notice that we are still defining sin θ as `"opp"/"hyp"`;




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download




How To Take The Derivative Of Tan X Video Lesson Transcript Study Com
Start studying Pre Calc unit 4 Learn vocabulary, terms, and more with flashcards, games, and other study toolsSec2(2x) sec 2 ( 2 x) Because the two sides have been shown to be equivalent, the equation is an identity tan2(2x)sin2(2x) cos2(2x) = sec2 (2x) tan 2 ( 2 x) sin 2 ( 2 x) cos 2 ( 2 x) = sec 2 ( 2 x) is an identityFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
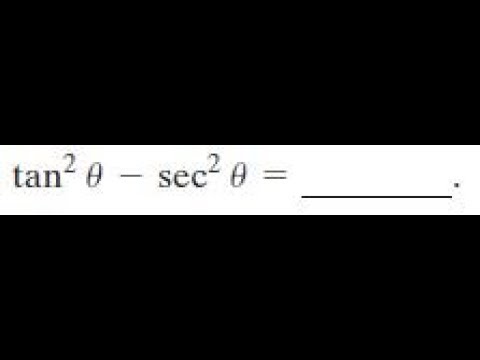



Tan 2x Sec 2x Youtube
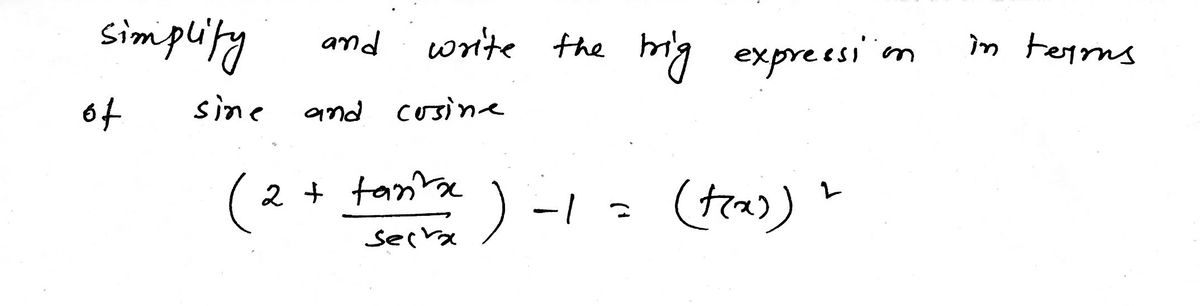



Answered Simplify And Write The Trig Expression Bartleby
To express the remaining factors in terms of cosine Then substitute Note that if the powers of both sine and cosine are odd, either (a) or (b) can be used d dx tan x sec2x sec2x x tanmx secnx dx sin x cos x 1 2 sin 2x cos2x 1 sin2x 2 1 cos 2x 1 2 1 cos 2x u cos x y 1 cos2x k cosnx sin x dx y sin2k1 x cosnx dx y sin 2x k cosnx sin x dxIn Trigonemetry Laws and Identities, there are some rule that we will use to prove 1 / sec² (x) = cos² (x) * tan² (x) 1 = sec² (x) * sin² (x) cos² (x) = 1 * tan (x) = sin (x) / cos (x) We will prove from the Left Hand Side We know that sec²Quotient Identities tan(x)= sin(x) cos(x) and cot(x)= cos




Integral Of Secant Cubed Wikipedia



1
Math\sin^2x\cos^2x=1/math math\implies\dfrac{\sin^2x}{\cos^2x}\dfrac{\cos^2x}{\cos^2x}=\dfrac{1}{\cos^2x}/math math\implies\left(\dfrac{\sin x}{\cos x√画像をダウンロード tan^2xsec^2x in terms of sine and cosine Tan^2xsec^2x in terms of sine and cosineRewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x)




Derivative Rules For Trigonometric Functions




Powers Of Trigonometric Functions
How do you verify the equation is an identity?Solution for Establish the identity cos u tan u sec u = 1 sin u Write the left side in terms of sine and cosine tan u secu =Solve the following equation {eq}tan (2x) sec (2x) = cos (x) sin (x) {/eq} Trigonometric Ratio We know that rightangled triangles have three sides;




Reciprocal Identities In Trigonometry With Examples Owlcation




Trigonometric Identities Ppt Download
Simplify and write the trigonometric expression in terms of sine and cosine tan^2 xsec^2 x= math Rewrite the expression as an algebraic expresion in x tan(sin−1x)= Math Rewrite the expression in terms of the first power of the cosine sin^8(x) how do i do this plz help !!These are the hypotenuse, base, and Simplify and write the trigonometric expression in terms of sine and cosine (2tan^2x / sec^2x) 1 = (f (x))^2




Section 7 3 Double Angle Half Angle And Sum




Sec 4 X Sec 2 X Tan 4 X Tan 2 X Youtube
Start studying Pre Calculas Trig Identities Learn vocabulary, terms, and more with flashcards, games, and other study toolsTurn all functions into sin x and cos x secr smx esc x 3 Substitution of identity sin 2 x cos 2 x tan 2 x sec 2 x 2 Conjugate I — cos x sum x smx I cos x 1 Algebra techniques utilized (cotx cscx) (cos x 1) (sint cos t)21 sm x a c d OIL" ing OIL" ing distribution example 1 examp e 2 2 sect csct sm t cost sec t csc t (tan t



3




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic
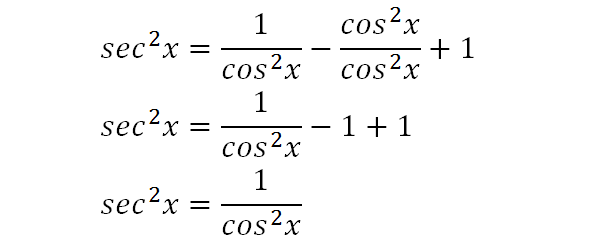



Integrate Sec 2x Method 2




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download




7 2 Pre Class Assignment Power Reducing Formulas 1 Chegg Com




How To Find The Inverse Of A Trig Function Dummies




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby
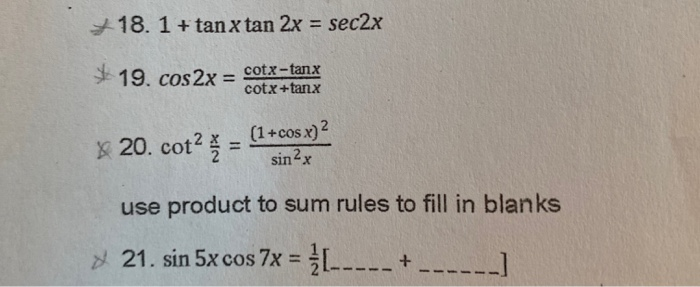



18 1 Tan X Tan 2x Sec2x 19 Cos2x Cotx Tank Chegg Com
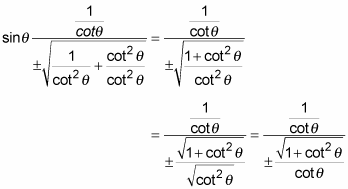



Express Sine In Terms Of Cotangent Dummies




Directions Simplify The Given Trigonometric Expr Gauthmath




Trig Integrals Trig Substitution



If Cos X 1 2 Then What Is The Value Of Tan 2x Quora




Trigonometry




Factor The Expression Then Use Fundamental Identities To Simplify Cos 2x Sec 2x Cos 2x Study Com
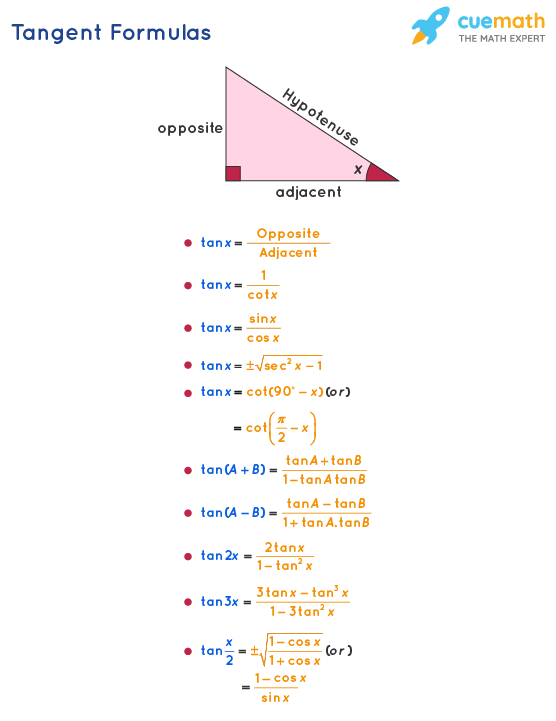



Tangent Formula What Are Tangent Formulas Examples
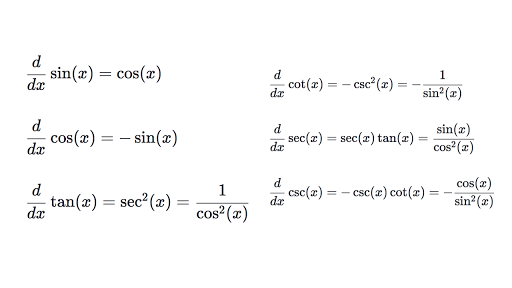



Differentiating Trigonometric Functions Review Article Khan Academy




Derive 1 Tan 2x Sec 2x And 1 Cot 2x Text Cosec 2x Geometrically Mathematics Stack Exchange



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero



How To Write Tan In Terms Of Sin




Integrate Sec 2x Method 2
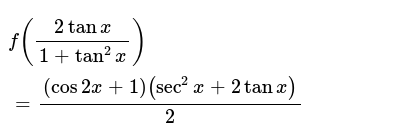



F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2




Write The Expression In Terms Of Sine And Cosine And Chegg Com




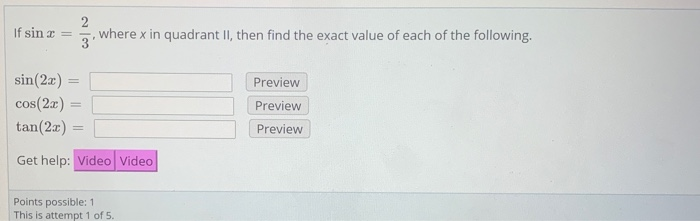
Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



What Trigonometric Identity Should I Use To Simplify 1 Tanx Secxtanx Secx Sec 2x 1 Tanx 2 The Answer Is Secx Tanx 1 1 Tanx 2 But Having Trouble Simplifying The Problem To Get The Answer Quora




Simplify This Trig Function 1 Tan 2x Csc 2x Youtube




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Answered Power Reducing Formulas Cos 2x 1 Cos Bartleby




Tangent Half Angle Formula Wikipedia




Verify Each Trigonometric Equation By Substituting Identities To Match The Right Hand Side Of The Brainly Com




Is There Any Other Way To Establish This Trig Identity Frac Sec X 1 Tan X Frac Sin X 1 Cos X Mathematics Stack Exchange




Simplify And Write The Trigonometric Expression In Chegg Com




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download




Tangent Half Angle Formula Wikipedia




Weierstrass Substitution Wikipedia




14 2 Trigonometric Identities



Derivatives Of Trigonometric Functions




List Of Trigonometric Identities Wikipedia




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Write Tan X In Terms Of Sec X Study Com



What Are The Quotient Identities For A Trigonometric Functions Socratic
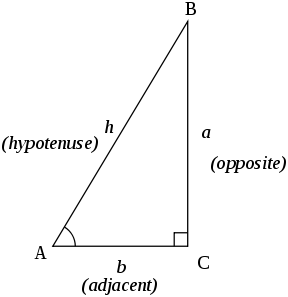



Basic Trigonometric Functions Trigonometry Socratic




7 2 Trigonometric Integrals Ppt Download
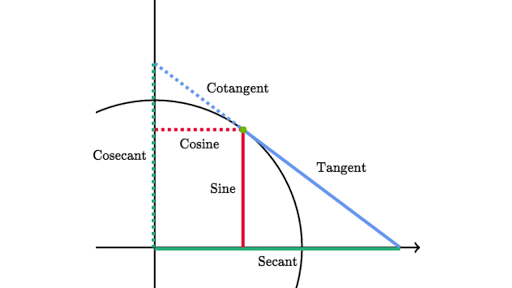



Trig Identity Reference Article Khan Academy




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube
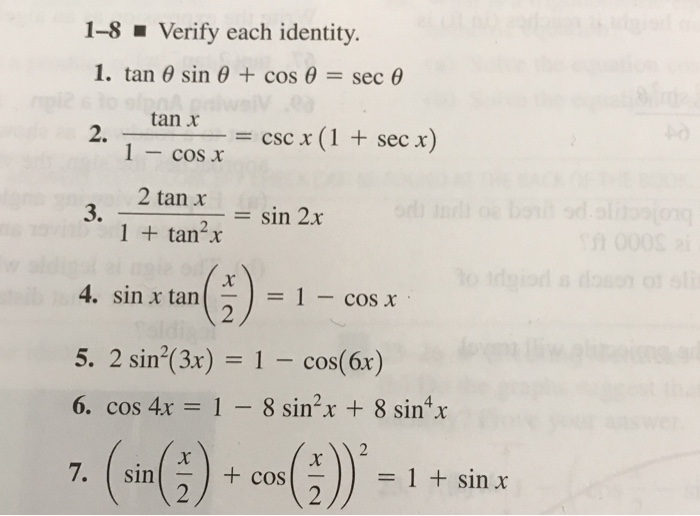



1 8 Verify Each Identity Sec 8 1 Tan 8 Sin 8 Chegg Com




Verify That The Equation Is An Identity 1 Tan X Chegg Com




Math34 Trigonometric Formulas




Trigonometric Identities And Equations




Using Trigonometric Identities Video Khan Academy




Power Reducing Formulas And How To Use Them With Examples Owlcation




Trigonometric Functions Introduction Sine Cosine Videos And Examples



6 1 2 Trigonometric Identities



bestpictjcry Tan 2x Tan 2x




Powers Of Trigonometric Functions




How To Find Least Value Of Cos 2 X Sec 2 X Quora




Derive 1 Tan 2x Sec 2x And 1 Cot 2x Text Cosec 2x Geometrically Mathematics Stack Exchange




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube




Verify That The Equation Is An Identity 1 Tan X Chegg Com




Analytic Trig Ppt Video Online Download



Simplify And Write The Trigonometric Expression In Chegg Com




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube
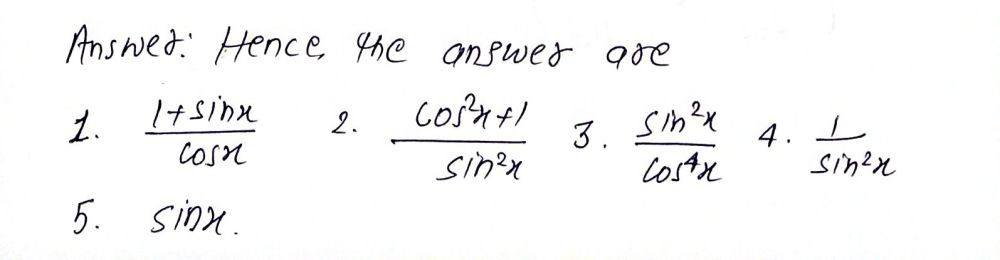



Directions Simplify The Given Trigonometric Expr Gauthmath




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



What Is The Identity Tan 2x Equal To In Terms Of Sinx And Cosx Quora




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube



1




Trigonometry Reciprocal Identities Expii
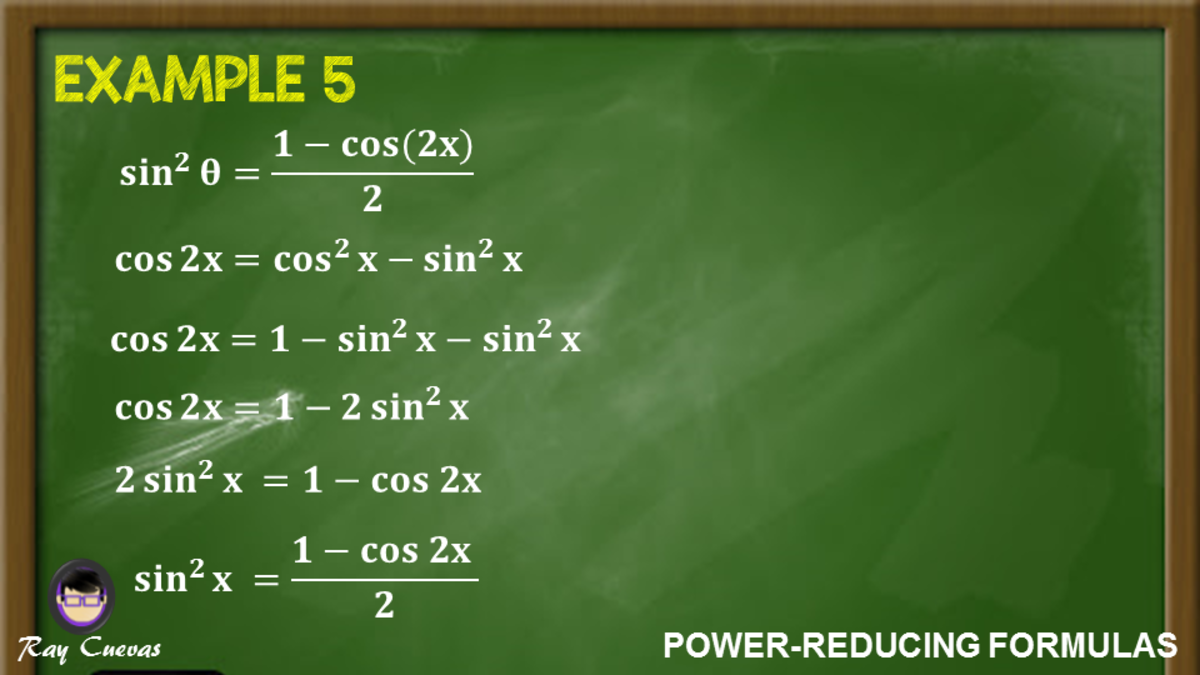



Power Reducing Formulas And How To Use Them With Examples Owlcation




Chapter 9 Notes



1




14 2 Trigonometric Identities




Weierstrass Substitution Wikipedia



How Do We Prove That Tan2x 1 Sec2x Tanx Quora



What Is The Formula Of Tan2x Quora



Pdf Trigonometric Integrals Jerome Delen Academia Edu
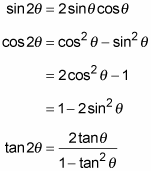



How Do You Prove That Cot2x Tan 2x 1 2tanx Socratic




Trig Identity Sec2x Minus Tan2x T10 Youtube



0 件のコメント:
コメントを投稿